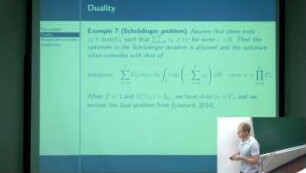
Approximation of optimal convex shapes with applications in optimal insulation

Abstract: In the optimization of convex domains under a PDE constraint numerical difficulties arise in the approximation of convex domains in higher dimensions. Previous research used a restriction to rotationally symmetric domains to reduce shape optimization problems to a two-dimensional setting. In the current research, two approaches for the approximation in three dimensions are considered. First, a notion of discrete convexity allows for a nearly convex approximation with polyhedral domains. In the relaxation to discrete convex domains, the regularity of boundaries of convex domains is lost. This is noticeable when considering more complex shape optimization problems. However, with further assumptions on the discrete domains, sufficient convergence results can be proven which imply stability of shape optimization problems.

An alternative is based on the recent observation that higher order finite elements can approximate convex functions conformally. As a second approach these results are used to approximate optimal convex domains with isoparametric convex domains. The proposed algorithms are tested on shape optimization problems constraint by a Poisson equation and eigenvalue problems in optimal insulation and approximated consistent results.

The main application lies in a problem in optimal insulation for which a surprising breaking of symmetry occurs. An eigenvalue problem arising in optimal insulation related to the minimization of the heat decay rate of an insulated body is adapted and positive lower bound on the distribution of insulating material is imposed. We prove the existence of optimal domains among a class of convex domains, propose a numerical scheme to approximate the eigenvalue and prove the stability of the discrete shape optimization. To observe how the lower bound affects the breaking of symmetry in the optimal insulation and the shape optimization, the eigenvalue and optimal domains are approximated for several values of mass of insultating material and positive lower bounds

Object Details

• Location: Deutsche Nationalbibliothek Frankfurt am Main
• Extent: Online-Ressource
• Language: Englisch
• Notes: Universität Freiburg, Dissertation, 2024

Classification and Topics

• Keyword: Konvexe Optimierung ; Approximation ; Gestaltoptimierung ; Optimale Kontrolle ; Variationsrechnung ; Optimierung ; Optimale Kontrolle

Contributors, Places and Time

• Event: Veröffentlichung
• (where): Freiburg
• (who): Universität
• (when): 2024
• Creator: Keller, Hedwig
• Contributor: Bartels, Sören ; Bartels, Sören ; Antil, Harbir ; Albert-Ludwigs-Universität Freiburg. Fakultät für Mathematik und Physik

Further information

• DOI: 10.6094/UNIFR/256312
• URN: urn:nbn:de:bsz:25-freidok-2563127
• Rights: Open Access; Der Zugriff auf das Objekt ist unbeschränkt möglich.
• Last update: 25.03.2025, 1:45 PM CET