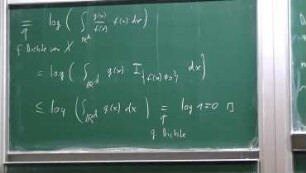Exact maximum-likelihood method to detect patterns in real networks

Arbeitspapier

In order to detect patterns in real networks, randomized graph ensembles that preserve only part of the topology of an observed network are systematically used as fundamental null models. However, their generation is still problematic. The existing approaches are either computationally demanding and beyond analytic control, or analytically accessible but highly approximate. Here we propose a solution to this long-standing problem by introducing an exact and fast method that allows to obtain expectation values and standard deviations of any topological property analytically, for any binary, weighted, directed or undirected network. Remarkably, the time required to obtain the expectation value of any property is as short as that required to compute the same property on the single original network. Our method reveals that the null behavior of various correlation properties is different from what previously believed, and highly sensitive to the particular network considered. Moreover, our approach shows that important structural properties (such as the modularity used in community detection problems) are currently based on incorrect expressions, and provides the exact quantities that should replace them.

Object Details

• Language: Englisch

References and Relationships

• Bibliographic citation: Series: LEM Working Paper Series ; No. 2011/07

Classification and Topics

• Classification: Wirtschaft

Contributors, Places and Time

• Event: Geistige Schöpfung
• (who): Squartini, Tiziano ; Garlaschelli, Diego
• Event: Veröffentlichung
• (who): Scuola Superiore Sant'Anna, Laboratory of Economics and Management (LEM)
• (where): Pisa
• (when): 2011

Further information

• Handle: http://hdl.handle.net/10419/89455
• Last update: 10.03.2025, 11:43 AM CET