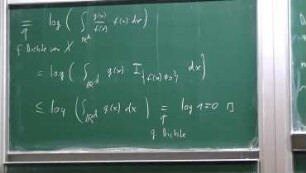Artikel
Lasso maximum likelihood estimation of parametric models with singular information matrices
An information matrix of a parametric model being singular at a certain true value of a parameter vector is irregular. The maximum likelihood estimator in the irregular case usually has a rate of convergence slower than the Ín-rate in a regular case. We propose to estimate such models by the adaptive lasso maximum likelihood and propose an information criterion to select the involved tuning parameter. We show that the penalized maximum likelihood estimator has the oracle properties. The method can implement model selection and estimation simultaneously and the estimator always has the usual Ín-rate of convergence.
- Sprache
-
Englisch
- Erschienen in
-
Journal: Econometrics ; ISSN: 2225-1146 ; Volume: 6 ; Year: 2018 ; Issue: 1 ; Pages: 1-24 ; Basel: MDPI
- Klassifikation
-
Wirtschaft
Estimation: General
Methodological Issues: General
Model Construction and Estimation
Model Evaluation, Validation, and Selection
- Thema
-
penalized maximum likelihood
singular information matrix
lasso
oracle properties
- Ereignis
-
Geistige Schöpfung
- (wer)
-
Jin, Fei
Lee, Lung-Fei
- Ereignis
-
Veröffentlichung
- (wer)
-
MDPI
- (wo)
-
Basel
- (wann)
-
2018
- DOI
-
doi:10.3390/econometrics6010008
- Handle
- Letzte Aktualisierung
-
10.03.2025, 11:45 MEZ
Datenpartner
Dieses Objekt wird bereitgestellt von:
ZBW - Deutsche Zentralbibliothek für Wirtschaftswissenschaften - Leibniz-Informationszentrum Wirtschaft. Bei Fragen zum Objekt wenden Sie sich bitte an den Datenpartner.
ZBW - Deutsche Zentralbibliothek für Wirtschaftswissenschaften - Leibniz-Informationszentrum Wirtschaft. Bei Fragen zum Objekt wenden Sie sich bitte an den Datenpartner.
Objekttyp
- Artikel
Beteiligte
- Jin, Fei
- Lee, Lung-Fei
- MDPI
Entstanden
- 2018
Ähnliche Objekte (12)
Maximum-Likelihood-Schätzer
Maximum-Likelihood-Verfahren
Pseudo-variance quasi-maximum likelihood estimation of semi-parametric time series models
Parametric statistical models and likelihood
Maximum approximated likelihood estimation
Maximum Likelihood Phylodynamic Analysis
Sieve maximum likelihood estimation in a semi-parametric regression model with errors in variables
Maximum-Likelihood-Decodierung von Faltungscodes
Maximum likelihood and economic modeling
Maximum Likelihood Estimation of Search Costs
Maximum-likelihood estimation of multipath channels
Maximum likelihood estimation of functional relationships
Maximum-Likelihood-Schätzer
Maximum-Likelihood-Verfahren
Pseudo-variance quasi-maximum likelihood estimation of semi-parametric time series models
Parametric statistical models and likelihood
Maximum approximated likelihood estimation
Maximum Likelihood Phylodynamic Analysis
Sieve maximum likelihood estimation in a semi-parametric regression model with errors in variables
Maximum-Likelihood-Decodierung von Faltungscodes
Maximum likelihood and economic modeling
Maximum Likelihood Estimation of Search Costs
Maximum-likelihood estimation of multipath channels
Maximum likelihood estimation of functional relationships
Maximum-Likelihood-Schätzer
Maximum-Likelihood-Verfahren
Pseudo-variance quasi-maximum likelihood estimation of semi-parametric time series models
Parametric statistical models and likelihood
Maximum approximated likelihood estimation
Maximum Likelihood Phylodynamic Analysis
Sieve maximum likelihood estimation in a semi-parametric regression model with errors in variables
Maximum-Likelihood-Decodierung von Faltungscodes
Maximum likelihood and economic modeling
Maximum Likelihood Estimation of Search Costs
Maximum-likelihood estimation of multipath channels