Mathematisches Modell
Minimaler Knotenkasten
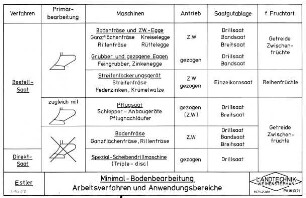
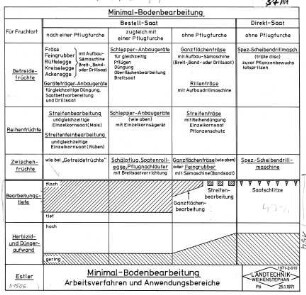
Kurzbeschreibung: Das Modell zeigt das Bild einer Fläche in der dreidimensionalen Sphäre S^3 mit ausgezeichneten Eigenschaften unter einer stereographischen Projektion.
Modellbeschreibung:
- Die Fläche ist eine unberandete verzweigte Minimalfläche in S^3. Der Verzweigungsort ist ein Kreis. Wird dieser entfernt bleibt ein Möbiusband übrig.
- Sie ist ein Deformationsretrakt des Komplements des Kleeblattknotens.
- Sie ist der Schnittort eines Kleeblattknotens in S^3, d.h. der Ort aller Punkte, von denen mindestens zwei Punkte des Knotens denselben minimalen Abstand haben.
- Sie ist hochsymmetrisch (invariant unter einer ein-Parametergruppe von Isometrien der S^3.
- In der natürlichen Parametrisierung sind die einen Parameterlinien Kreisbögen, die die anderen Parameterlinien orthogonal schneiden. Diese sind (bis auf den Verzweigungskreis) Kleeblattknoten.
- Standort
-
Technische Universität Dresden, Institut für Geometrie
- Sammlung
-
Mathematische Modelle, Technische Universität Dresden
- Maße
-
20 x 15 x 9,5 (in cm)
255 (in g)
- Material/Technik
-
3-D-Druck auf Gipsbasis
- Klassifikation
-
Topologie (Fachgebiet)
Differentialgeometrie (Fachgebiet)
- Bezug (was)
-
einseitige Flächen
Minimalflächen
Knoten
- Ereignis
-
Entwurf
- (wer)
-
Brehm (Entwerfer)
- Letzte Aktualisierung
-
25.03.2025, 11:48 MEZ
Datenpartner
Dieses Objekt wird bereitgestellt von:
Institut für Geometrie der Technischen Universität Dresden. Bei Fragen zum Objekt wenden Sie sich bitte an den Datenpartner.
Institut für Geometrie der Technischen Universität Dresden. Bei Fragen zum Objekt wenden Sie sich bitte an den Datenpartner.
Objekttyp
- Mathematisches Modell
Beteiligte
- Brehm (Entwerfer)
Ähnliche Objekte (12)
One2one : minimal space, minimal housing
Minimal and hyper-minimal biautomata
Minimal
Minimal Media Art – Minimal Music (Steve Reich)
Minimal architecture
Minimal-Bodenbearbeitung
Minimal Dog
Minimal-Bodenbearbeitung
Minimal-Bestellkombination
Minimal plus
Minimal lernen
Minimal art
One2one : minimal space, minimal housing
Minimal and hyper-minimal biautomata
Minimal
Minimal Media Art – Minimal Music (Steve Reich)
Minimal architecture
Minimal-Bodenbearbeitung
Minimal Dog
Minimal-Bodenbearbeitung
Minimal-Bestellkombination
Minimal plus
Minimal lernen
Minimal art
One2one : minimal space, minimal housing
Minimal and hyper-minimal biautomata
Minimal
Minimal Media Art – Minimal Music (Steve Reich)
Minimal architecture
Minimal-Bodenbearbeitung
Minimal Dog
Minimal-Bodenbearbeitung
Minimal-Bestellkombination
Minimal plus
Minimal lernen